Sudoku Variations

Ed Pegg Jr., September 6, 2005 (updated Sep 15)

In the May 1979 issue of Dell Pencil Puzzles & Word Games (issue #16), page 6, something amazing appeared: Number Place. Here are the original instructions: "In this puzzle, your job is to place a number into every empty box so that each row across, each column down, and each small 9-box square within the large square (there are 9 of these) will contain each number from 1 through 9. Remember that no number may appear more than once in any row across, any column down, or within any small 9-box square; this will help you solve the puzzle. The numbers in circles below the diagram will give you a head start--each of these four numbers goes into one of the circle boxes in the diagram (not necessarily in the order given)."

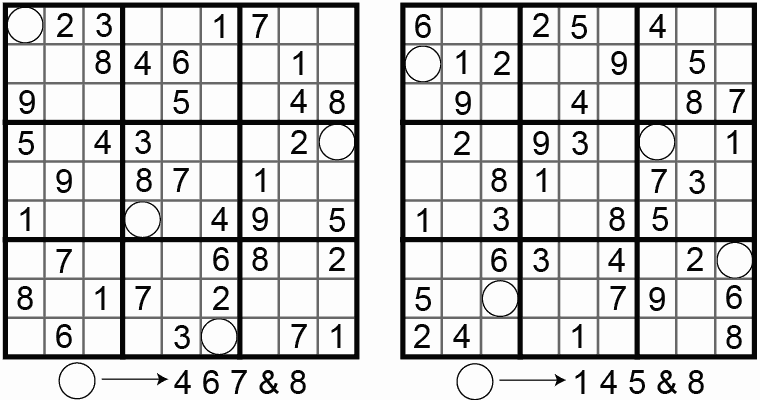
Figure 1. The first Number Place puzzles. (Dell Pencil Puzzles & Word Games #16, page 6, 1979-05)

Who made this puzzle? In addition to being the crossword editor of the New York Times, Will Shortz is a puzzle historian, so he did detective work to find the answer. He knew that "Number Place" puzzles had appeared in Dell Magazines, and went through his collection to find the first. Dell listed no author, but the name Howard Garns always appeared in the contributor's list of any issue containing a "Number Place" puzzle. Also, Garns' name did not appear in any issue lacking a Number Place, which clinched the identification. Further research revealed that Howard Garns to be a retired architect who created the puzzle at age 74. Howard Garns died in Indianapolis in 1989, and never got a chance to see his creation as a worldwide phenomenon. (Shortz, pers. comm. 2005)

Howard Garns made many Number Place puzzles for Dell, quickly simplifying the rules to those used today -- Fill in the grid so that every row, column, and 3x3 box contains the digits 1 through 9. In April 1984, Japan's puzzle group Nikoli discovered Dell’s Number Place presented it for a Japanese audience in the pages of puzzle paper Monthly Nikolist. Originally named Suuji Wa Dokushin Ni Kagiru, ("the numbers must be single") the puzzle became very popular. Kaji Maki, the president of Nikoli, abbreviated it to Sudoku - (Su = number, Doku = single), and trademarked the name. As the popular grew, competing companies stayed with the non-trademarked name Number Place, or "nanpure". Even today, many Japanese puzzle magazines spell out "Number Place" in English. In the United States and elsewhere, it's called Sudoku ("single number" in Japanese). Thus, japanese-speakers use the English, and english-speakers use the Japanese. Here are two particularly nice Sudoku puzzles under the normal rules.

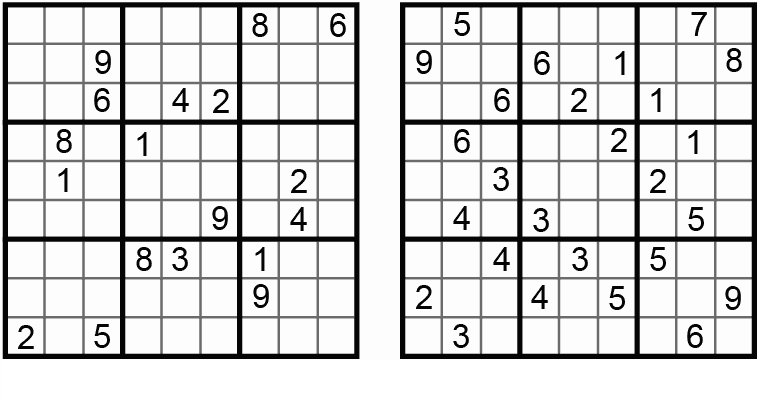
Figure 2. Two normal Sudoku/Number Place/Nanpure puzzles. (Reader submissions to Nanpure Fan, 2004-10)

The first puzzle above is worth noting for being a symmetrical number place with only 18 given cells. The minimum known number of givens leading to a unique solution is 17. Graph theorist Gordon Royle has collected over ten thousand (danger! huge page!) non-equivalent Sudoku puzzles with 17 givens. The second puzzle above has a pleasing arrangement of given numbers in the center.

Within the many Sudoku sites, the classic rules predominate. Sudoku X, Samaria Sudoku, and other sizes are the only other variants I could find outside of World Puzzle Championship competitions. I decided to look for more variants, and tried my hand at creating a few myself. First, Sudoku X.

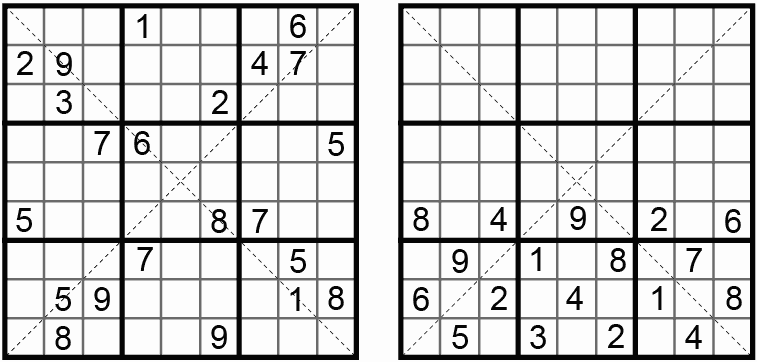
Figure 3. Diagonal Number Place. Ranking Puzzler #2 2002-08-20, Nanpure Fan #52 2004-10.

In Diagonal Sudoku, fill in the grid so that every row, column, 3x3 box, and main diagonal contains the digits 1 through 9. This variant is also called taikakusen nanpure, Diagonal Line Number Place, Sudoku X, Kokonotsu, or Dell's Number Place Challenger. I'm not sure what the minimal number of givens is for Diagonal Sudoku. The first "Number Place" puzzles with diagonal constraints was invented by Walter Mackey, appearing in Dell Champion in the early 1990s.

Figure 4. Even-Odd Number Place (Guusuu Kisuu Nanpure). Nanbaapureesu (Number Place) 2004-09. Gray cells are even, white cells are odd.

Even-Odd Sudoku: Fill in the grid so that every row, column, 3x3 box, contains the digits 1 through 9, with gray cells even, white cells odd. I haven't seen Even-Odd Sudoku on any site. Again, the minimum number of givens would be an interesting problem.

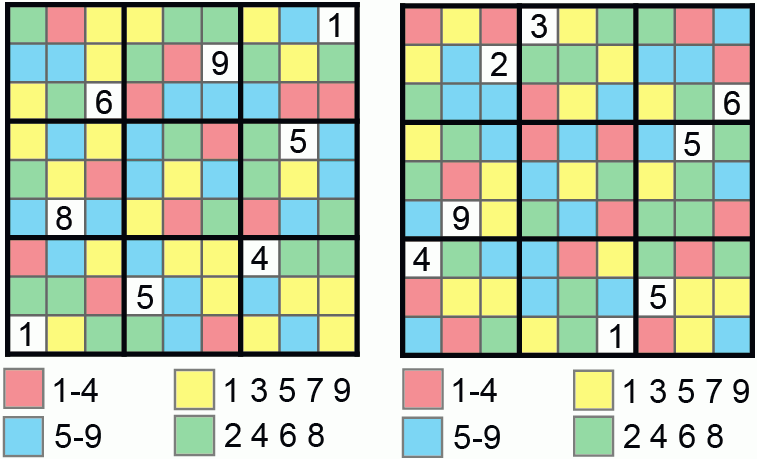
Figure 5. Big-small-even-odd Number Place (Daishou Guusuu Kisuu Nanpure). Nanpure Fan #51 2004-08.

Various colored Sudoku have appeared. In the above, coloring restricts what can be placed in a cell. Other variants use color to delineate extra regions. I call it "Extra Regions Sudoku" in the finale puzzle. Nanbaapureesu calls it Two-Tone Color Number Place (Tsuuton Karaa Nanpure). In these, extra regions are shaded in with a color. These regions each contain all the digits 1-9.

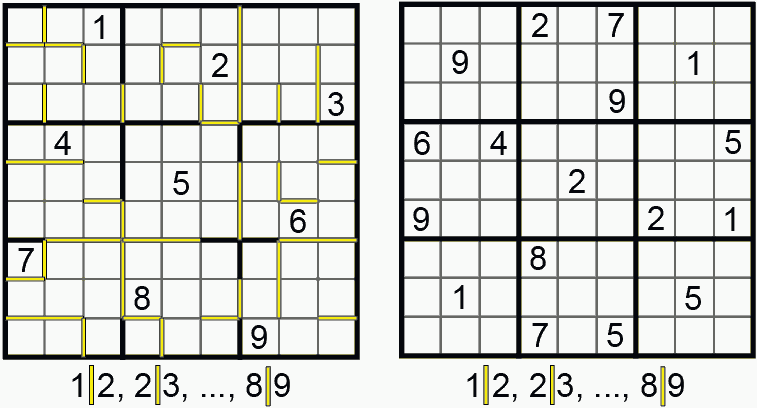
Figure 6. 1-away Disallowed Number Place (Hitotsu Chigai Nanpure). Nanpure Fan #52 2004-10.

In Consecutive Sudoku (or 1-away Disallowed Number Place), all the places where orthogonally adjacent cells are consecutive numbers have been specially marked. Note that the second puzzle is completely unmarked -- this is deliberate! Puzzles with a single given are possible.

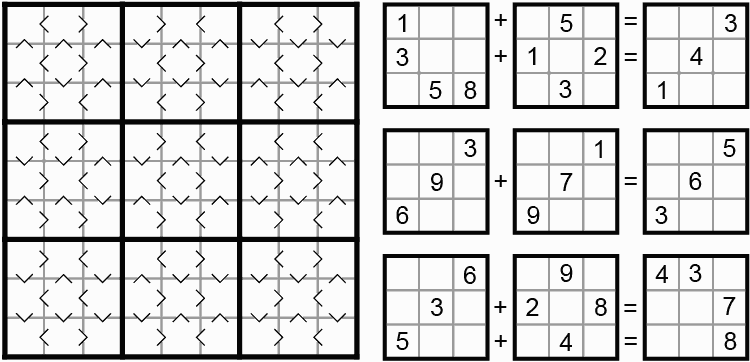
Figure 7. Greater Than Sudoku (Puzzler 1999-11) and Sums Sudoku by Ed Pegg Jr.

Greater Than Sudoku, or simply ">", doesn't have any given numbers at all. I've been struggling with it for a good 4 hours now, and still haven't solved it, but I've had to use all sorts of novel logic to make progress, so it's a good one. The second was inspired by Alastair Cuthbertson, who mentioned hiding pandigital sums in a Sudoku, like 357 + 624 = 981. I wrote a Mathematica program to find the maximum number of pandigital sums in a Sudoku (5). Incidentally, I found the three Mathematica Sudoku solvers mentioned in the MathWorld entry quite useful in checking some of these puzzles, and for checking a few hundred thousand generated puzzles.

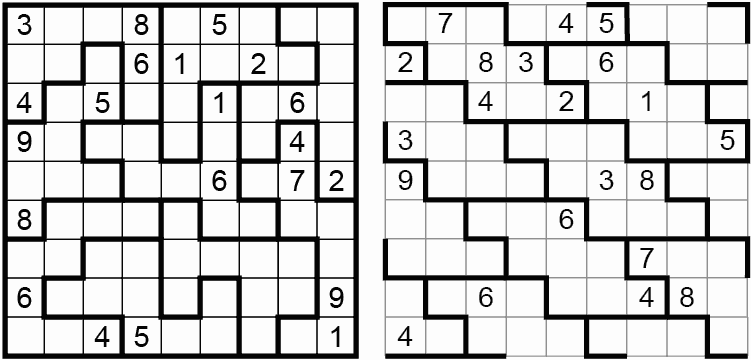
Figure 8. Geometry Number Place (kikagaku nanpure). WPC 9 (Stamford) and 2005 USPC, both by Michael Rios.

In Geometry Sudoku, irregular regions replace the boxes. In the second puzzle above, the grid is toroidal, and wraps around on both edges. The only trick here is that the regions are of odd shapes. These have also been called Latin Squares Puzzles.

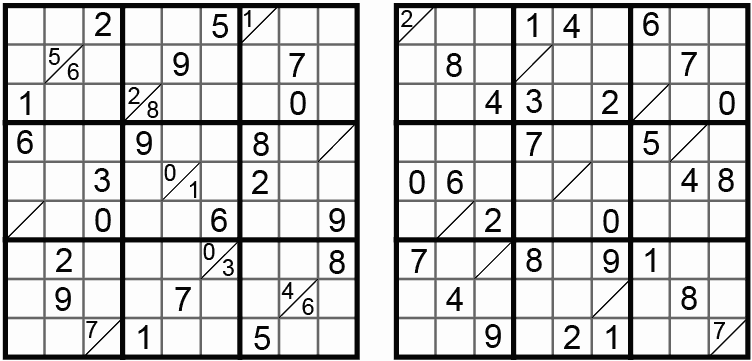
Figure 9. 0 to 9 Number Place (Zero Tuu Nain Nanpure). Nanpure Fan #52 2004-10.

In 0 to 9 Number Place, each row, column, and region has all 10 digits. Some cells contain two digits, and those are marked. The same puzzle where the two-digit cells didn't get marked would probably be much more difficult than a regular Sudoku puzzle.

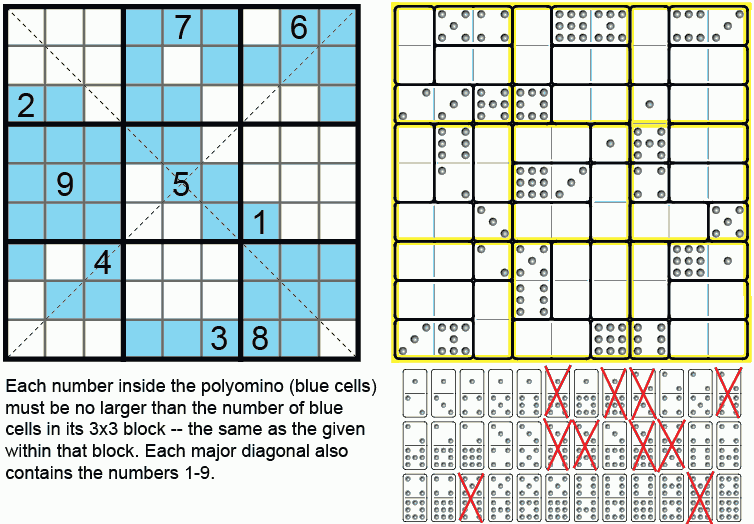
Figure 10. (a) Magic Sudoku, by Alexandre Owen Muniz (b) Domino Sudoku by Ed Pegg Jr. Use all the dominoes to make Sudoku.

Magic Sudoku inspired this column. Note that the 9 givens make a magic square, that the blue regions are all connected, and that there are five blue cells on each line. Despite satisfying extraordinary constraints, it's a very nice puzzle. After solving it, I started wondering if a set of dominoes+monominoes could be used to make a Sudoku. I constructed the puzzle above entirely by hand, because my program was getting nowhere. I'm hoping to make a 16x16 Domino Sudoku out of a double-15 set sans doubles and a 4x4 magic square.

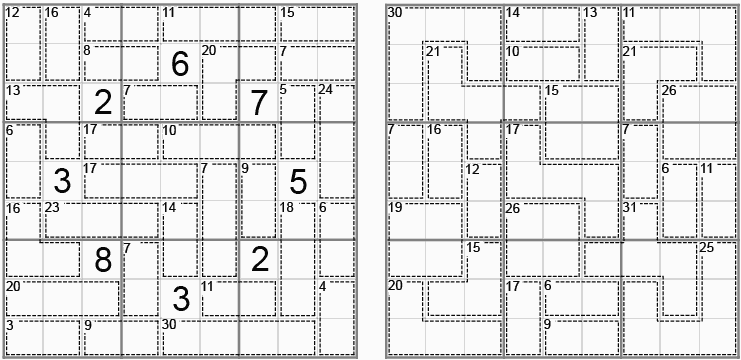
Figure 11. Sums Number Place (samu nanpure) (Puzzler 2002-02), Killer Sudoku by Tetsuya Nishio (London Times 2005-08).

In Sums Sudoku, sub-regions have specified sums, and no number can be repeated within a region. Tetsuya Nishio now makes these for the Times. With Nishio's efforts in the mid-1980's, and his later creation of Paint by Numbers puzzles, grid-style logic puzzles became very popular in Japan.

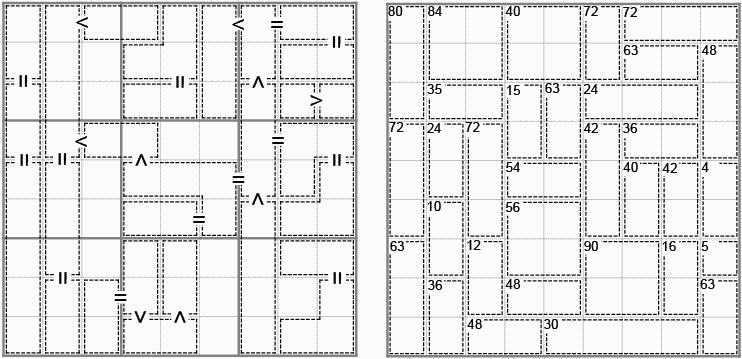
Figure 12. Sums Number Place. Nanpure Fan #51 2004-08. Factor Rooms (inshi no heya) by Yano Ryuou, Nikoli #92, 2000-09.

The first puzzle here is a Nanpure Fan reader submission. There are sub-regions given, and mathematical signs describe the relationships between the *sums* of the numbers in those regions. This is likely the most difficult puzzle within this column.

Issue 92 of Nikoli (2000-09) introduced a puzzle called Factor Rooms invented by Yano Ryuou. The goal is to create a 9x9 Latin square by filling each cell with digits from 1 through 9. Regions are given, and the *product* of the numbers in the regions are given. "Factor Rooms" puzzles have appeared sporadically in Nikoli since issue 95.

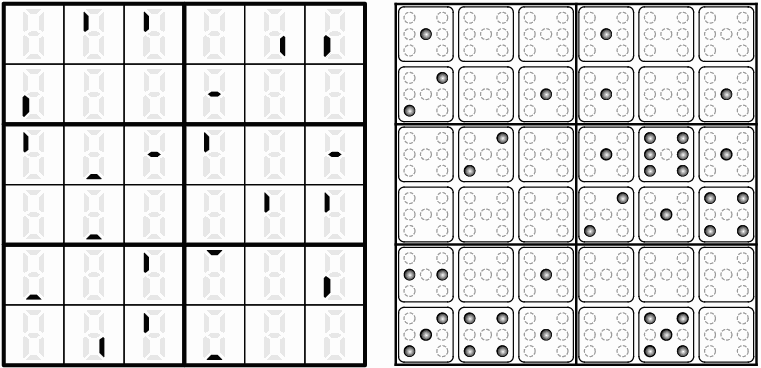
Figure 13. Digit Place by Cihan Altay, 2005 USPC. Pips Number Place (Puzzler 1999-04)

Not all puzzles use 1 to 9. Using just 1 to 6 is also possible. In the first puzzle above, the finished puzzle has numbers like those on a digital clock. In the second puzzle, the numbers are given by pips, like those seen in dice or dominoes.

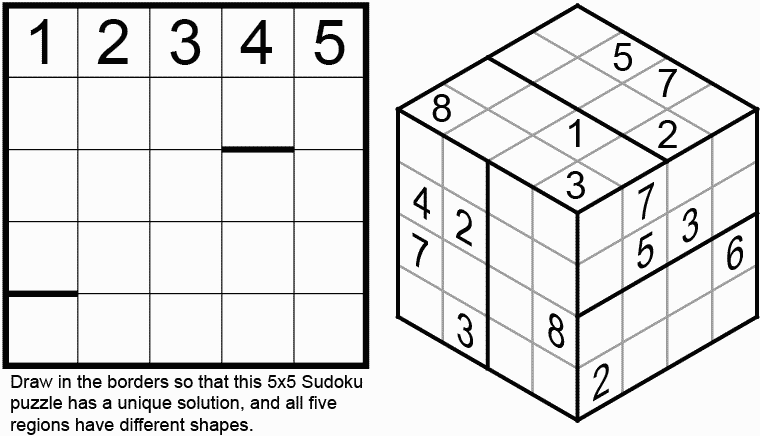
Figure 14. Meta Sudoku by Wei-Hwa Huang. Cubic Sudoku (Puzzler 1999-04)

The first puzzle is a "Meta" puzzle -- you must fill in the other borders (two are given) so that the resulting Sudoku puzzle has a unique solution. In Cubic Sudoku, the constraints on the cubic portion is that each region has digits from 1 through 8, each "layer" of the three dimensions on the cube also have distinct digits.

The London Times popularized Samurai Sudoku, which has 5 Sudoku joined in a quincunx arrangement. For the last puzzle of the column, here is five variants in one puzzle.

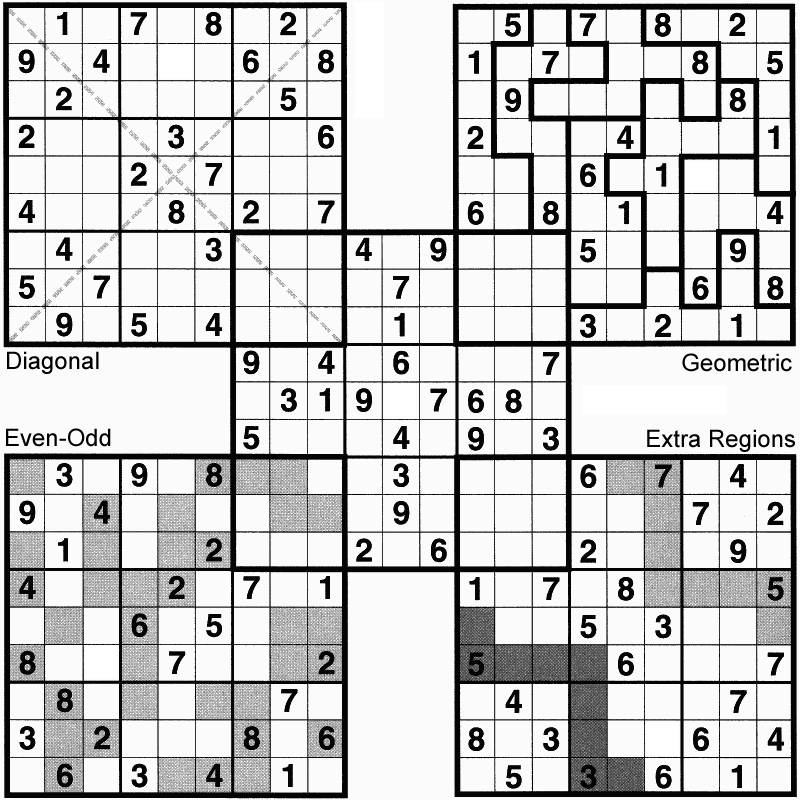
Figure 15. Combined Number Place (gattai nanpure). Nanbaapureesu (Number Place) 2004-09.

This puzzle is a 5-way hybrid! (Diagonal, Extra Regions, Geometric, Combined, and Even-Odd).

Some other variants that have been published are:

1-5, each three times, in each row, column, and region (12345 nanpure).
one 1, two 2s, three 3s, and four 4s in each region, row, and column (1234 nanpure). Identical digits are never orthogonally adjacent.
1-9 and three black cells in each row, column, and region (Kuro-masu Tsuki Nanpure = Black-cell Handling). The black cells have to obey Japanese crossword rules: no two are orthogonally adjacent, and they can't divide the grid up into two regions.
"Sweating Relay", or Progressive Sudoku: Three progressively larger Combined Number Places. Each time you solve a puzzle, you have to propagate certain digits to seed the next puzzle (this is the "relay" component). Here's a sample.
Word Sudoku. Letters replace numbers.
There are two variants I'd particularly like to see made.

Chess Sudoku. The digits 1-8 and a chess piece in each row, column, and region. Each piece should attack the numbers 1-8 exactly once.
16x16 Domino Sudoku. A set of Double-15 dominoes and a 4x4 magic square to make a Sudoku.
I'm sure Howard Garns would be pleased to see what his creation has wrought. If you'd like a nice printout of all these puzzles, here's a handy 8-page PDF file. In case you need help, here are the answers, by Alan O'Donnell. If you need more, here are my source files.

I'd like to thank Will Shortz, Nick Baxter, and Wei-Hwa Huang for their tremendous help in researching this column.

Conceptis Puzzles, "History of Sudoku," http://www.conceptispuzzles.com/articles/sudoku/.

Leo Lewis, "Try Killer Sudoku," http://www.timesonline.co.uk/article/0,,7-1757275,00.html.

Nikoli Puzzles, "Sudoku Outline," http://www.nikoli.co.jp/puzzles/1/index_text-e.htm.

Gordon Royle, "Sudoku Patterns," http://www.csse.uwa.edu.au/~gordon/sudokupat.php.

Will Shortz, "Sudoku Easy," St. Martin's Press, 2005.

Sudoku Forum, http://sudoku.jouwpagina.nl/. (A listing of many Sudoku links)

Sudoku Forum, "A Variety of Sudoku Variants," http://www.sudoku.com/forums/viewtopic.php?t=995.

"Sudoku", http://en.wikipedia.org/wiki/Sudoku.

Eric W. Weisstein et al. "Sudoku." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Sudoku.html.